TUGAS: 2017

SISTEM BILANGAN

I. DEFINISI

System bilangan (number system) adalah suatu cara untuk mewakili besaran dari suatu item fisik. Sistem bilanan yang banyak dipergunakan oleh manusia adalah system biilangan desimal, yaitu sisitem bilangan yang menggunakan 10 macam symbol untuk mewakili suatu besaran.Sistem ini banyak digunakan karena manusia mempunyai sepuluh jari untuk dapat membantu perhitungan. Lain halnya dengan komputer, logika di komputer diwakili oleh bentuk elemen dua keadaan yaitu off (tidak ada arus) dan on (ada arus). Konsep inilah yang dipakai dalam sistem bilangan binary yang mempunyai dua macam nilai untuk mewakili suatu besaran nilai.

Selain system bilangan biner, komputer juga menggunakan system bilangan octal dan hexadesimal.

II. Teori Bilangan

1. Bilangan Desimal

Sistem ini menggunakan 10 macam symbol yaitu 0,1,2,3,4,5,6,7,8,dan 9. system ini menggunakan basis 10. Bentuk nilai ini dapat berupa integer desimal atau pecahan.

Integer desimal :

adalah nilai desimal yang bulat, misalnya 8598 dapat diartikan :

8 x 10³ = 8000

5 x 10² = 500

9 x 10¹ = 90

8 x 10^{0 = 8}
^{+ 8598}

Absolue value (8598) merupakan nilai untuk masing-masing digit bilangan, sedangkan position value (10^n ) adalah merupakan penimbang atau bobot dari masing-masing digit tergantung dari letak posisinya, yaitu nernilai basis dipangkatkan dengan urutan posisinya.

Pecahan desimal :

Adalah nilai desimal yang mengandung nilai pecahan dibelakang koma, misalnya nilai 183,75 adalah pecahan desimal yang dapat diartikan :

misalnya nilai 183,75 adalah pecahan desimal yang dapat diartikan :

1 x 10 ² = 100

8 x 10 ¹ = 80

3 x 10 ⁰ = 3

7 x 10 ^–1 = 0,7
5 x 10 ^{–2 = 0,05}

^{+ 183,75}

2. Bilangan Binar

Sistem bilangan binary menggunakan 2 macam symbol bilangan berbasis 2digit angka, yaitu 0 dan 1.

Contoh bilangan 1001 dapat diartikan :

Operasi aritmetika pada bilangan Biner :

a. Penjumlahan

Dasar penujmlahan biner adalah :

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 0 dengan carry of 1, yaitu 1 + 1 = 2, karena digit terbesar ninari 1, maka harus dikurangi dengan 2 (basis), jadi 2 – 2 = 0 dengan carry of 1

contoh :

b. Pengurangan

Bilangan biner dikurangkan dengan cara yang sama dengan pengurangan bilangan desimal. Dasar pengurangan untuk masing-masing digit bilangan biner adalah :

dengan langkah – langkah :

c. Perkalian

Dilakukan sama dengan cara perkalian pada bilangan desimal. Dasar perkalian bilangan biner adalah :

0 x 0 = 0

1 x 0 = 0

0 x 1 = 0

1 x 1 = 1

contoh :

d. pembagian

Pembagian biner dilakukan juga dengan cara yang sama dengan bilangan desimal. Pembagian biner 0 tidak mempunyai arti, sehingga dasar pemagian biner adalah :

0 : 1 = 0

1 : 1 = 1

3. Bilangan Oktal

Sistem bilangan Oktal menggunakan 8 macam symbol bilangan berbasis 8 digit angka, yaitu 0 ,1,2,3,4,5,6,7.

Position value system bilangan octal adalah perpangkatan dari nilai 8.

Contoh :

Operasi Aritmetika pada Bilangan Oktal

a. Penjumlahan

Langkah-langkah penjumlahan octal :

- tambahkan masing-masing kolom secara desimal

- rubah dari hasil desimal ke octal

- tuliskan hasil dari digit paling kanan dari hasil octal

- kalau hasil penjumlahan tiap-tiap kolom terdiri dari dua digit, maka digit paling kiri merupakan carry of untuk penjumlahan kolom selanjutnya.

Contoh :

b. Pengurangan

Pengurangan Oktal dapat dilaukan secara sama dengan pengurangan bilangan desimal.

Contoh :

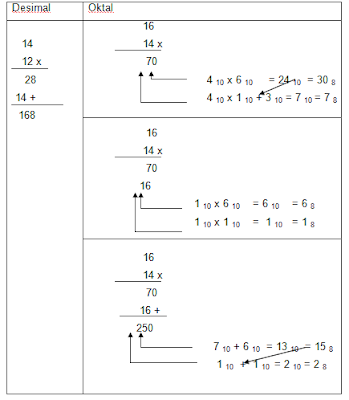
c. Perkalian

Langkah – langkah :

- kalikan masing-masing kolom secara desimal

- rubah dari hasil desimal ke octal

- tuliskan hasil dari digit paling kanan dari hasil octal

- kalau hasil perkalian tiap kolol terdiri dari 2 digit, maka digit paling kiri merupakan carry of untuk ditambahkan pada hasil perkalian kolom selanjutnya.

Contoh :

d. Pembagian

4. Bilangan Hexadesimal

Sistem bilangan Oktal menggunakan 16 macam symbol bilangan berbasis 8 digit angka, yaitu 0 ,1,2,3,4,5,6,7,8,9,A,B,C,D,Edan F

Dimana A = 10, B = 11, C= 12, D = 13 , E = 14 dan F = 15

Position value system bilangan octal adalah perpangkatan dari nilai 16.

Contoh :

Operasi Aritmetika Pada Bilangan Hexadesimal

a. Penjumlahan

Penjumlahan bilangan hexadesimal dapat dilakukan secara sama dengan penjumlahan bilangan octal, dengan langkah-langkah sebagai berikut :

Langkah-langkah penjumlahan hexadesimal :

- tambahkan masing-masing kolom secara desimal

- rubah dari hasil desimal ke hexadesimal

- tuliskan hasil dari digit paling kanan dari hasil hexadesimal

- kalau hasil penjumlahan tiap-tiap kolom terdiri dari dua digit, maka digit paling kiri merupakan carry of untuk penjumlahan kolom selanjutnya.

Contoh :

b. Pengurangan

Pengurangan bilangan hexadesimal dapat dilakukan secara sama dengan pengurangan bilangan desimal.

Contoh :

c. Perkalian

Langkah – langkah :

- kalikan masing-masing kolom secara desimal

- rubah dari hasil desimal ke octal

- tuliskan hasil dari digit paling kanan dari hasil octal

- kalau hasil perkalian tiap kolol terdiri dari 2 digit, maka digit paling kiri merupakan carry of untuk ditambahkan pada hasil perkalian kolom selanjutnya.

Contoh :

d. Pembagian

Contoh :

III. Konversi Bilangan

Konversi bilangan adalah suatu proses dimana satu system bilangan dengan basis tertentu akan dijadikan bilangan dengan basis yang alian.

Konversi dari bilangan Desimal

1. Konversi dari bilangan Desimal ke biner

Yaitu dengan cara membagi bilangan desimal dengan dua kemudian diambil sisa pembagiannya.

Contoh :

2. Konversi bilangan Desimal ke Oktal

Yaitu dengan cara membagi bilangan desimal dengan 8 kemudian diambil sisa pembagiannya

3. Konversi bilangan Desimal ke Hexadesimal

Yaitu dengan cara membagi bilangan desimal dengan 16 kemudian diambil sisa pembagiannya

Contoh :

Konversi dari system bilangan Biner

1. Konversi ke desimal

Yaitu dengan cara mengalikan masing-masing bit dalam bilangan dengan position valuenya.

Contoh :

2. Konversi ke Oktal

Dapat dilakukan dengan mengkonversikan tiap-tiap tiga buah digit biner yang dimulai dari bagian belakang.

Contoh :

Begitu seterusnya untuk yang lain.

3. Konversi ke Hexademial

Dapat dilakukan dengan mengkonversikan tiap-tiap empat buah digit biner yang dimulai dari bagian belakang.

Contoh :

Konversi dari system bilangan Oktal

1. Konversi ke Desimal

Yaitu dengan cara mengalikan masing-masing bit dalam bilangan dengan position valuenya.

Contoh :

2. Konversi ke Biner

Dilakukan dengan mengkonversikan masing-masing digit octal ke tiga digit biner.

Contoh :

6502 (8) ….. = (2)

2 = 010

0 = 000

5 = 101

6 = 110

jadi 110101000010

3. Konversi ke Hexadesimal

Dilakukan dengan cara merubah dari bilangan octal menjadi bilangan biner kemudian dikonversikan ke hexadesimal.

Contoh :

2537 (8) = …..(16)

2537 (8) = 010101011111

010101010000(2) = 55F (16)

Konversi dari bilangan Hexadesimal

1. Konversi ke Desimal

Yaitu dengan cara mengalikan masing-masing bit dalam bilangan dengan position valuenya.

Contoh :

2. Konversi ke Oktal

Dilakukan dengan cara merubah dari bilangan hexadesimal menjadi biner terlebih dahulu kemudian dikonversikan ke octal.

Contoh :

55F (16) = …..(8)

55F(16) = 010101011111(2)

010101011111 (2) = 2537 (8)

TEOREMA SUPERPOSISI

Dasar Teori :

Teorema Superposisi memberikan suatu konsep rangkaian yang penting. Dimana tiap sumber energy dipertimbangkan secara terpisah. Tiap-tiap efek kemudian dikombinasikan untuk memberikan efek total.

Konsep ini dapat digunakan untuk anbalisi rangkaian yang sederhana. Beberapa pedoman pada rangkaian dimana lebih cocok untuk analisis superposisi, yaitu :

1. Lebih dari satu sumber energy

2. Sumber tegangan atau sumber arus

3. Struktur rangkaian sempurna

Ada enam dasar operasi dalam penerapan teorema superposisi untuk menganalisa rangkaian :

1. Pilih satu sumber energy

2. Untuk sumber yang lain :

a. Sumber tegangan dihubung singkat ( short circuit)

b. Sumber arus di open circuit

3. Hitung resistansi

4. Tentukan arus atau tegangan tiap-tiap elemen. Catat arah dan polaritasnya.

5. Ulangi langkah 1 sampai 4 untuk sumber yang lain

6. Jumlahkan hasil masing-masing secara dialjabarkan

Pada teorema ini hanya berlaku untuk rangkaian yang bersifat linier, dimana rangkaian linier adalah suatu rangkaian dimana persamaan yang muncul akan memenuhi jika y = kx, dimana k = konstanta dan x = variabel.

Dalam setiap rangkaian linier dengan beberapa buah sumber tegangan/ sumber arusdapat dihitung dengan cara :

Menjumlah aljabarkan tegangan/ arus yang disebabkan tiap sumber independent/

bebas yang bekerja sendiri, dengan semua sumber tegangan/ arus independent/ bebas lainnya diganti dengan tahanan dalamnya.

Pengertian dari teorema diatas bahwa jika terdapat n buah sumber bebas maka dengan teorema superposisi samadengan n buah keadaan rangkaian yang dianalisis, dimana nantinya n buah keadaan tersebut akan dijumlahkan. Jika terdapat beberapa buah sumber tak bebas maka tetap saja teorema superposisi menghitung untuk n buah keadaan dari n buah sumber yang bebasnya.

Rangkaian linier tentu tidak terlepas dari gabungan rangkaian yang mempunyai sumber independent atau sumber bebas, sumber dependent / sumber tak bebas linier (sumber dependent arus/ tegangan sebanding dengan pangkat satu dari tegangan/ arus lain, atau sebanding dengan jumlah pangkat satu besaran-besaran tersebut) dan elemen resistor (R ), induktor ( L ), dan kapasitor ( C ).

Arus yang melalui, atau tegangan yang melintas sebuah elemen dalam sebuah jaringan linear dua arah sama dengan jumlah aljabar arus atau tegangan yang dihasilkan secara terpisah oleh masing-masing sumber. Arus total yang melalui sembarang bagian jaringan sama dengan jumlah aljabar arus yang dihasilkan secara terpisah yang tidak saling tergantung oleh masing-masing sumber.(Sebuah jaringan dengan dua sumber : jika arus yang dihasilkan oleh salah satu sumber memiliki arah tertentu, sedangkan yang dihasilkan oleh sumber yang lain berlawanan arah yang melalui tahanan yang sama, maka arus yang dihasilkan adalah perbedaan arus di antara keduanya dan memiliki arah mengikuti yang lebih besar. Jika arus yang dihasilkan memiliki arah yang sama, maka arus yang dihasilkan adalah jumlah keduanya.)

Prinsip Superposisi tidak dapat digunakan untuk perhitungan daya karena daya yang hilang dalam sebuah sumber tahanan berubah-ubah sebanding dengan kuadrat arus atau tegangan (tidak linear). Untuk memperhatikan pengaruh masing-masing sumber secara terpisah yang tidak bergantung sama lain, maka sumber tersebut perlu diambil dan ditempatkan kembali tanpa mempengaruhi hasil akhir. Untuk mengambil sumber tegangan, maka perbedaan potensial antara terminal sumber tegangan harus ditetapkan berharga nol (dihubung singkat). Untuk mengambil sumber arus, maka diperlukan bahwa terminalnya terbuka (untai terbuka). Sembarang hambatan dalam yang berhubungan dengan sumber yang dicabut, tidak dihilangkan tetapi masih harus diperhatikan.

Pengaruh pengambilan sumber praktis : Pengaruh pengambilan sumber ideal :

Contoh 1 :

Tentukan I₁ untuk jaringan :

Penggantian Sumber Tegangan, menghitung I’₁ dengan Aturan Pembagi Arus.

Penggantian Sumber Arus, menghitung I’’₁dengan Hukum Ohm.

Karena I’₁dan I’’₁memiliki arah yang sama, maka arus I₁sama dengan jumlah arus keduanya.

I₁ = I’₁ + I’’₁ = 0 A + 5 A = 5 A

Teorema superposisi berlaku untuk semua rangkaian linear dan bilateral. Dalam teorema superposisi ini terdapat dua atau lebih sumber yang bebas. Sumber tersebut bisa tegangan dengan tegangan dan bisa tegangan dengan arus. Sumber-sumber tersebut tidak dapat bekerja secara bersamaan atau hanya berpatokan pada satu sumber saja. Sumber-sumber ini bekerja satu persatu. Sumber-sumber tegangan yang akan di tahan sewaktu salah satu sumber lain (sumber tunggal) bekerja digantikan oleh rangkaian hubung singkat (short), sumber-sumber arus digantikan dengan rangkaian terbuka (o.c). Teorema superposisi digunakan untuk menghitung besar arus pada masing-masing beban dengan menentukan terlebih dahulu arah arus pada rangkaian. Dibawah ini adalah contoh gambar rangkaian listrik yang dapat di analisis dengan metode atau teorema superposisi.

Sifat- Sifat Teorema Superposisi :

Berpatokan pada satu sumber, sumber (E) yang lain di hubung singkat (short) atau jika pada arus (I) dalam rangkaian terbuka (o.c)
Tidak berpengaruh dengan sumbernya
Besar I₃ akan sama dengan I 1/3 + I 2/3 apabila searah
Jika I 1/2 > I 2/2 maka I 1/2 - I2/2 atau sebaliknya

Langkah Percobaan

Menghitung arus dengan dua sumber tegangan.

1. Berpatokan pada V₁dan pada V₂di short.

· Cari arus yang dihasilkan oleh V₁ saja. Ganti sumber tegangan V₂ dengan hubung singkat.

_·Carilah arus pada I₁¹ dengan menggantikan R_1,R₂dan R₃menjadi R₄

· Setelah R_T di ketahui maka I₁¹, I₂¹, I₃¹ dapat di cari

2. Bepatokan pada V₂saja dan pada V₁di short

· Cari arus yang dihasilkan oleh V₂ saja. Ganti sumber tegangan V₁ dengan hubung singkat.

_·Carilah arus pada I₁² dengan menggantikan R_1,R₂dan R₃menjadi R₅

Setelah R_T di ketahui maka I₁², I₂², I₃² dapat di cari dengan formula dibawah ini:

a. Menghitung arus menggunakan sumber tegangan dan arus.

1. Berpatokan pada I dan E di hubung singkat

· Cari arus yang dihasilkan oleh I saja.

· Ganti sumber tegangan E dengan hubung singkat. (Lihat gambar di bawah ini)

I 1/3 tidak dicari karena tidak ada arus yang melewati R₃

2. Berpatokan pada sumber tegangan (E)

· Cari arus yang dihasilkan oleh tegangan E saja.

· Ganti arus I dengan rangkaian terbuka (o.c)

Dari gambar di atas akan di dapat suatu formulasi sebagai berikut :

Diagram Rangkaian

Penyelesaian :

Jawaban :

Pada saat sumber tegangan aktif/bekerja maka sumber arus tidak aktif (diganti dengan

tahanan dalamnya yaitu tak hingga atau rangkaian open circuit) :

Pada saat sumber arus aktif/bekerja maka sumber tegangan tidak aktif (diganti dengan

tahanan dalamnya yaitu nol atau rangkaian short circuit) :

2 .

Jawaban :

Pada saat sumber Vs = 17V aktif/bekerja maka sumber tegangan 6 V diganti dengan

tahanan dalamnnya yaitu nol atau rangkaian short circuit, dan sumber arus 2 A diganti dengan tahanan dalamnya yaitu tak hingga atau rangkaian open circuit :

Pada saat sumber Vs = 6V aktif/bekerja maka sumber tegangan 17 V diganti dengan

tahanan dalamnnya yaitu nol atau rangkaian short circuit, dan sumber arus 2 A diganti dengan tahanan dalamnya yaitu tak hingga atau rangkaian open circuit :

Pada saat sumber Is = 2A aktif/bekerja maka sumber tegangan 17 V diganti dengan

tahanan dalamnnya yaitu nol atau rangkaian short circuit, dan sumber tegangan 6 V

diganti dengan tahanan dalamnya yaitu nol atau rangkaian short circuit :

Jawaban :

Pada rangkaian ini terdapat sumber tak bebasnya, maka tetap dalam perhitungan dengan teorema superposisi membuat analisis untuk n buah keadaan sumber bebas, pada soal diatas terdapat dua buah sumber bebas, maka dengan superposisi terdapat dua buah keadaan yang harus dianalisis.

Pada saat sumber Is = 8A aktif/bekerja maka sumber arus 4A diganti dengan tahanan

dalamnnya yaitu tak hingga atau rangkaian open circuit :